 |
Casual
Mind Magic – Deckbau
von Florian Koch |
28.05.2009 |

| -Bisher in dieser Reihe | |  |
| |
Willkommen zum neunten und letzten Teil dieser Reihe: Diesmal geht's um Deckbau im Mind Magic.
Wie geht man dieses Problem wohl an? Zunächst einmal sollte man sich vielleicht fragen, warum man überhaupt ein Deck bauen will und nicht einfach einen Stapel Karten nimmt, der irgendwo rumfliegt. Meine Antwort darauf ist, dass ich in meinem Deck keine Karten haben möchte, die mit 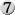  oder oder 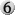 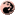 als Common zwar in den Stapel geraten können, aber leider nie irgendwas machen. als Common zwar in den Stapel geraten können, aber leider nie irgendwas machen.
Selbst weniger extreme Beispiele möchte man vermeiden, weil eine Karte, die immer nur ein oder zwei sinnvolle Anwendungen hat, sich auf Dauer sehr unspannend spielt. Um mal bei dem extremen Beispiel zu bleiben: 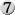  würde man zum Beispiel in jedem Spiel als Morph auslegen und das ist nicht nur langweilig, sondern auch wenig herausfordernd. würde man zum Beispiel in jedem Spiel als Morph auslegen und das ist nicht nur langweilig, sondern auch wenig herausfordernd.
Auf der anderen Seite gibt es über 300 Karten, die   kosten. Von diesen sind zwar nicht alle interessant, aber doch so viele, dass ich diese Spruchkosten gern mehrfach in meinem Deck haben möchte. Denn auch das vierte kosten. Von diesen sind zwar nicht alle interessant, aber doch so viele, dass ich diese Spruchkosten gern mehrfach in meinem Deck haben möchte. Denn auch das vierte   , das in einem Spiel gezogen wird, bietet häufig komplett andere Optionen als die drei Vorherigen, weil sich die Spielsituation verändert hat und die Karte entsprechend flexibel einsetzbar ist. Es gilt also das richtige Mischungsverhältnis zu finden: Für welche Karten gibt es so wenig Optionen, dass man sie gar nicht im Deck haben möchte und für welche so viele, dass man sie häufiger im Deck haben kann? Und wie häufig möchte man sie dann im Deck haben? , das in einem Spiel gezogen wird, bietet häufig komplett andere Optionen als die drei Vorherigen, weil sich die Spielsituation verändert hat und die Karte entsprechend flexibel einsetzbar ist. Es gilt also das richtige Mischungsverhältnis zu finden: Für welche Karten gibt es so wenig Optionen, dass man sie gar nicht im Deck haben möchte und für welche so viele, dass man sie häufiger im Deck haben kann? Und wie häufig möchte man sie dann im Deck haben?
Erste Überlegungen
Um diese Fragen zu beantworten, muss man sich überlegen, wovon es überhaupt abhängt, wie flexibel eine Karte ist. Zumindest grob hängt es offensichtlich von der Anzahl der Karten ab, die es in diesem Manaslot gibt. Während es 300 Karten für   gibt, existieren nur drei, die gibt, existieren nur drei, die 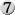  kosten. Ist kosten. Ist   also hundertmal so flexibel wie also hundertmal so flexibel wie 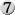  ? Das ist schwer zu beantworten. Von den ? Das ist schwer zu beantworten. Von den 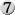  -Karten sind zwei spielbar, aber wie viele -Karten sind zwei spielbar, aber wie viele   -Karten sind realistisch spielbar? Obwohl es einige offensichtliche gute Kandidaten (Negate) und einige offensichtlich schlechte Kandidaten (Vodalian Soldiers) gibt, ist nicht klar, wie viele Optionen man tatsächlich hat. -Karten sind realistisch spielbar? Obwohl es einige offensichtliche gute Kandidaten (Negate) und einige offensichtlich schlechte Kandidaten (Vodalian Soldiers) gibt, ist nicht klar, wie viele Optionen man tatsächlich hat.
Da es sehr schwierig sein dürfte, eine vernünftige Antwort auf diese Frage zu finden, besinnen wir uns am besten auf die einzige Näherung, die wir haben: Die Anzahl der Karten in dem Slot. Die logische Herangehensweise ist also, den Gatherer zu fragen, wie viele Karten es in den Manaslots gibt und das Deck dann mit Karten in dem Verhältnis zu füllen, wie sie auch in der Realität auftauchen.
Auszählungsverfahren 101
Schauen wir zunächst mal nach, wie häufig es verschiedene blaue Karten in Legacy gibt. (Mind Magic mit dem Vintage-Kartenpool ist ziemlich unsinnig.) mit dem Vintage-Kartenpool ist ziemlich unsinnig.)
 | 1 |
 | 178 |
  | 313 |
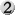  | 287 |
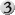  | 178 |
  | 84 |
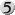  | 29 |
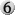  | 7 |
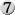  | 3 |
  | 53 |
   | 83 |
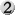   | 115 |
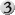   | 86 |
   | 36 |
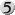   | 22 |
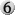   | 8 |
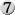   | 3 |
   | 3 |
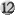   | 1 |
   | 7 |
    | 1 |
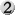    | 6 |
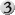    | 6 |
    | 8 |
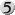    | 4 |
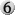    | 4 |
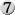    | 3 |
    | 1 |
    | 1 |
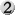     | 1 |
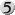     | 1 |
| | |
| | 1568 |
Kleiner Einschub für eine neue Trivia-Runde: Welche Karten verbergen sich hinter den einzigartigen Manakosten?
Was fängt man damit an? Es gibt ein praktisches Verfahren, das ein Holländer namens D'Hondt erfunden hat. Er hat sich das ausgedacht, um zu bestimmen, wie viele Sitze Parteien im Parlament erhalten sollen. Der Deutsche Bundestag hat das früher verwendet, aber es funktioniert auch für unsere Zwecke. Das läuft folgendermaßen: Man schreibt hinter jede Partei die Anzahl der Stimmen, die sie bekommen hat. Dahinter schreibt man dann die Anzahl der Stimmen geteilt durch zwei, durch drei usw. Wenn man das hinreichend oft gemacht hat, vergibt man für die größten X Zahlen in dieser Tabelle jeweils einen Sitz, wobei X natürlich der Gesamtzahl der Sitze entspricht.
Wir können das Gleiche tun, nur dass wir die Parteien durch die verschiedenen Manaslots ersetzen und die Anzahl der Sitze im Parlament durch die Anzahl der Karten in unserem Deck. Das haben wir aber noch gar nicht diskutiert: Wie groß soll das Deck denn sein? Alles ist möglich, aber ich verwende 120 Karten, weil sich das angenehm in zwei Decks Š 60 Karten aufteilen lässt und mit dieser Anzahl fühlt man sich als Magic-Spieler wohl. Im Prinzip kann das Deck aber auch jede andere Größe haben.
Bevor wir anfangen, machen wir uns die Sache noch ein wenig leichter: Eigentlich müsste man diese Rechnung für alle Manakosten gleichzeitig anstellen, ich verzichte mal darauf und weise jeder Farbe 18 Plätze zu. Das lässt noch 30 Slots für Artefakte, Länder und bunte Karten. Die zweite Vereinfachung ist, dass ich die 5%-Hürde an unsere Zwecke anpasse. Karten mit Manakosten, die weniger als zehnmal auftauchen, werden einfach nicht berücksichtigt. Das ändert nichts am Ergebnis, ich muss aber nicht so viel schreiben und Ihr nicht so riesige Tabellen lesen. Also dann:
 | 178 | 89 | 59,33 | 44,5 | |
  | 313 | 156,5 | 104,33 | 78,25 | 62,6 |
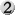  | 287 | 143,5 | 95,67 | 71,75 | 57,4 |
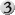  | 178 | 89 | 59,33 | | |
  | 84 | 42 | | | |
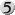  | 29 | | | | |
  | 53 | | | | |
   | 83 | 41,5 | | | |
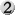   | 115 | 57,5 | | | |
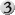   | 86 | 43 | | | |
   | 36 | | | | |
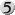   | 22 | | | | |
Die fettgedruckten Zahlen entsprechen den 17 höchsten Zahlen. Unglücklicherweise sind  und und 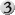  als Kandidaten für den letzten Slot gleich auf. Was tut man in solchen Fällen? Bei Stimmengleichheit entscheidet der Großwesir... Es zwingt einen sowieso niemand dazu, sich sklavisch an dieses Ergebnis zu halten, aber an dieser Stelle bietet es sich an, nach eigenem Geschmack zu entscheiden. Weniger gefällt mir an diesem Ergebnis, dass die Slots mit vielen Karten sehr stark vertreten sind, andere dafür gar nicht. So macht als Kandidaten für den letzten Slot gleich auf. Was tut man in solchen Fällen? Bei Stimmengleichheit entscheidet der Großwesir... Es zwingt einen sowieso niemand dazu, sich sklavisch an dieses Ergebnis zu halten, aber an dieser Stelle bietet es sich an, nach eigenem Geschmack zu entscheiden. Weniger gefällt mir an diesem Ergebnis, dass die Slots mit vielen Karten sehr stark vertreten sind, andere dafür gar nicht. So macht   mehr als ein Viertel der blauen Karten aus, aber mehr als ein Viertel der blauen Karten aus, aber   und und   schaffen es nicht ins Deck, obwohl es für sie durchaus viele gute Einsatzmöglichkeiten gibt. Was ist da zu tun? Nach russischem Brauch das Parlament auflösen und neu wählen lassen? schaffen es nicht ins Deck, obwohl es für sie durchaus viele gute Einsatzmöglichkeiten gibt. Was ist da zu tun? Nach russischem Brauch das Parlament auflösen und neu wählen lassen?
Eigengewächs


Die sinnvolle Alternative ist, ein anderes Auszählverfahren anzuwenden. Es gibt da reichlich Auswahl: Hare-Niemeyer, Sainte-LaguŽ, Hill-Huntington usw. Wir können uns aber auch einfach ein Verfahren selbst stricken. Meine Idee war, anstatt durch 1, 2, 3,..., n zu teilen, durch 2^0, 2^1, 2^2,..., 2^n zu teilen. Der Vorteil davon sollte sein, dass es für einen Manaslot immer schwieriger wird, zusätzliche Plätze im Deck zu bekommen, während es auf der anderen Seite leichter wird, zumindest einen Slot zu bekommen. Bei D'Hondt hingegen wird es mit steigender Größe vergleichsweise leichter an zusätzliche Slots zu kommen. Und das Ergebnis?
 | 178 | 89 | 44,5 | 22,25 | 11,125 |
  | 313 | 156,5 | 78,25 | 39,125 | 19,5625 |
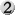  | 287 | 143,5 | 71,75 | 35,875 | 17,9375 |
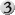  | 178 | 89 | 44,5 | 22,25 | 11,125 |
  | 84 | 42 | 21 | 10,5 | |
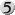  | 29 | 14,5 | | | |
  | 53 | 26,5 | 13,25 | | |
   | 83 | 41,5 | 20,75 | 10,375 | |
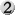   | 115 | 57,5 | 28,75 | 14,375 | |
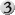   | 86 | 43 | 21,5 | 10,75 | |
   | 36 | 18 | | | |
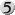   | 22 | 11 | | | |
Sieht trotz aller Überlegung gar nicht so viel anders aus. Die Unterschiede würden wohl stärker zu Tage treten, wenn man mehr Karten ins Deck steckte. Was mir insbesondere gar nicht gefällt ist, dass    noch immer nicht im Deck ist. Tatsächlich hat es überhaupt nur noch immer nicht im Deck ist. Tatsächlich hat es überhaupt nur   zusätzlich ins Deck geschafft, während sonst zumindest die Verteilung etwas gleichmäßiger geworden ist. zusätzlich ins Deck geschafft, während sonst zumindest die Verteilung etwas gleichmäßiger geworden ist.
Was haben wir nun noch für Möglichkeiten, um zumindest    noch ins Deck zu bekommen? Wir können die Anzahl der blauen Karten erhöhen, entweder indem wir den Anteil der farbigen Karten am Deck erhöhen oder indem wir das Deck größer machen. Dann müssten wir die Anzahl der blauen Karten aber auf 23 aufblähen. Das Deck würde dann ein ganzes Stück größer. Das ist prinzipiell kein Problem und man kann problemlos auch mit einem 150-Karten-Deck spielen, aber das möchte ich gerade nicht tun. noch ins Deck zu bekommen? Wir können die Anzahl der blauen Karten erhöhen, entweder indem wir den Anteil der farbigen Karten am Deck erhöhen oder indem wir das Deck größer machen. Dann müssten wir die Anzahl der blauen Karten aber auf 23 aufblähen. Das Deck würde dann ein ganzes Stück größer. Das ist prinzipiell kein Problem und man kann problemlos auch mit einem 150-Karten-Deck spielen, aber das möchte ich gerade nicht tun.
Wir können aber    auch einfach per Dekret ins Deck berufen. Wer muss darunter leiden? Entweder auch einfach per Dekret ins Deck berufen. Wer muss darunter leiden? Entweder    wird die 19. blaue Karte und unser Deck wird ein wenig größer oder wir schmeißen einfach die Karte raus, die es so gerade eben noch ins Deck geschafft hat: wird die 19. blaue Karte und unser Deck wird ein wenig größer oder wir schmeißen einfach die Karte raus, die es so gerade eben noch ins Deck geschafft hat:
The loser is  and and 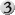  . Wieder stehen wir vor der Wahl... . Wieder stehen wir vor der Wahl...
Man kann diese Form des Minderheitenschutzes natürlich auch ausweiten. Wenn man der Meinung ist, 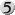  und und 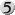   auch im Deck haben zu müssen, aber trotzdem nur 120 Karten spielen möchte, reserviert man eben für alle zwölf Manakosten jeweils einen Platz im Deck und verteilt dann, was übrig ist. Letztlich ist man ja eh frei darin, wie man sein Deck zusammenstellt, aber ich finde, dass mein Verfahren zumindest einen guten Ansatz dafür bietet, wie häufig welche Karten im Deck vertreten sein sollten. auch im Deck haben zu müssen, aber trotzdem nur 120 Karten spielen möchte, reserviert man eben für alle zwölf Manakosten jeweils einen Platz im Deck und verteilt dann, was übrig ist. Letztlich ist man ja eh frei darin, wie man sein Deck zusammenstellt, aber ich finde, dass mein Verfahren zumindest einen guten Ansatz dafür bietet, wie häufig welche Karten im Deck vertreten sein sollten.
Ausgezählt
Was kommt denn nun dabei heraus, wenn man mein Verfahren anwendet? Noch mal zur Erinnerung: Jede Farbe erhält 18 Slots, 15 bleiben für bunte und 15 für farblose Karten. (Und noch einmal zur Erinnerung: Bunte Karten empfehle ich so zu handhaben, dass man bei ihnen lediglich die Farbkombination, nicht aber die exakten Spruchkosten berücksichtigt.) zur Erinnerung: Bunte Karten empfehle ich so zu handhaben, dass man bei ihnen lediglich die Farbkombination, nicht aber die exakten Spruchkosten berücksichtigt.)
Wo ich schon einmal dabei bin: Bonustrivia! Welche Manakosten tauchen in Magic am häufigsten auf? Und eine Frage an das Forum: Sind die eingestreuten Trivias eher nette Abwechslung oder nervig?
Weiß:
3x  , 3x , 3x   , 3x , 3x 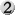  , 3x , 3x 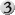  , 1x , 1x   , 1x , 1x   , 1x , 1x    , 2x , 2x 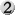   , 1x , 1x 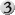  
Blau:
3x  , 3x , 3x   , 3x , 3x 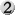  , 3x , 3x 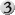  , 1x , 1x   , 1x , 1x   , 1x , 1x    , 2x , 2x 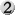   , 1x , 1x 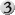  
Der ganze Aufwand, um dann identische Verteilungen zu bekommen? Mal schauen, ob das so weitergeht.
Schwarz:
2x  , 3x , 3x   , 3x , 3x 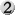  , 2x , 2x 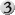  , 1x , 1x   , 1x , 1x   , 2x , 2x    , 2x , 2x 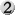   , 1x , 1x 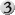   , 1x , 1x   
Rot:
3x 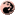 , 3x , 3x  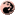 , 3x , 3x 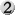 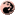 , 3x , 3x 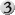 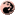 , 1x , 1x  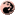 , 1x , 1x  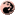 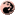 , 2x , 2x 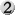 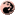 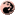 , 1x , 1x 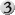 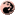 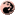 , 1x , 1x  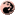 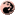
Grün:
3x  , 3x , 3x   , 3x , 3x 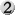  , 3x , 3x 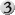  , 1x , 1x   , 1x , 1x    , 2x , 2x 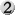   , 1x , 1x 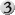   , 1x , 1x   
Riesig sind die Unterschiede zwischen den Farben nicht, aber ein paar kleine gibt es schon.
Multicolor:
2x WU, 2x UB, 2x BR, 2x RG, 2x GW, 1x WR, 1x UG, 1x BW, 1x RU, 1x GB
Colorless:
1x  , 3x , 3x 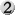 , 3x , 3x 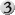 , 3x , 3x  , 1x , 1x 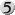 , 1x , 1x 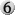 , 3x –/Land , 3x –/Land
Mit ein paar kleinen Unterschieden sieht mein Mind-Magic-Deck auch tatsächlich so aus. Ich mag die 4CC-Karten, außerdem finde ich null super. Deshalb sind bei mir    , ,    und und 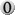 noch ins Deck gerutscht. noch ins Deck gerutscht.
Auflösung Trivia:
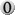 — Pact of Negation — Pact of Negation
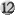   — Blinkmoth Infusion — Blinkmoth Infusion
    — Cryptic Command — Cryptic Command
    — Polar Kraken — Polar Kraken
    — Invoke Prejudice — Invoke Prejudice
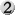     — Mind over Matter — Mind over Matter
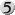     — Leviathan — Leviathan
  ist am häufigsten in Magic ist am häufigsten in Magic – der Allerweltszauber. – der Allerweltszauber.
Kommentiert.in unserem Forum
|
|















 Artikel |
Artikel |  News | Impressum | Datenschutzerklärung | Disclaimer | © by PlanetMTG 2025
News | Impressum | Datenschutzerklärung | Disclaimer | © by PlanetMTG 2025


 Artikel |
Artikel |  News | Impressum | Datenschutzerklärung | Disclaimer | © by PlanetMTG 2025
News | Impressum | Datenschutzerklärung | Disclaimer | © by PlanetMTG 2025